Smallest Baiocchi figures¶
Smallest Baiocchi figure (area 20):
Smallest known Baiocchi figure without holes (area 40):
Formulas¶
$N(w; h)$ - number of ways to tile $w\times h$ rectangle (including symmetric solutions)
$T(w; h) = \begin{cases} 1, & N(w; h) \geq 1 \\ 0, & \text{else} \end{cases}$ - tileability function, $1$ if tiles rectangle, $0$ otherwise
$A(w; h) = \left(N(w; h)\right)^{\frac{1}{wh}}$ - average number of ways to tile cell in $w\times h$ rectangle (including symmetric solutions)
$G(T; x; y) = \sum_{w=1}^{\infty}\sum _{h=1}^{\infty}T(w; h)x^wy^h$ - bivariate generating function of $T(w; h)$
$G(A; x; y) = \sum_{w=1}^{\infty}\sum _{h=1}^{\infty}A(w; h)x^wy^h$ - bivariate generating function of $A(w; h)$
$N(1; n) = T(1; n) = 0, \qquad n \geq 1 \tag{1}$
L pentomino has minimal dimension of $2$ thus it does not fit into $1 \times n$ rectangle. Q.E.D.
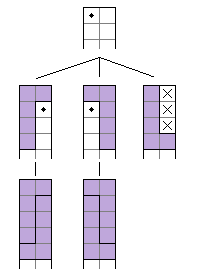
$N(2; n) = 2 \times N(2; n - 5), \qquad n \geq 6 \tag{2}$
If L pentomino tiles $2 \times n$ rectangle then all rectangle cells should filled. Top left corner (marked with dot on image) may be covered in only three ways. Only two of them are valid, because third leaves untileable cells (marked with crosses on image). When placing next pentomino in remaining two tilings, a $2 \times 5$ rectangle is covered. Remaining part is a $2 \times (n - 5)$ rectangle. So whole rectangle can be tiled in $2 \times N(2; n - 5)$ ways. Q.E.D.
$N(3; n) = T(3; n) = 0, \qquad n \geq 1 \tag{3}$
If L pentomino tiles $3 \times n$ rectangle then all rectangle cells should filled. Top left corner (marked with dot on image) may be covered in only three ways. Only two of them are valid, because third leave untileable hole (marked with cross on image). However, placing pentomino in first two ways is possible only in one way and then it also leaves untileable cells. Q.E.D.
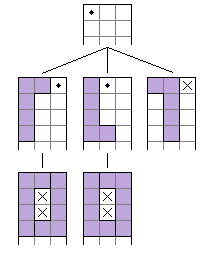
$N(4; n) = 4 \times N(4; n - 5), \qquad n \geq 6 \tag{4}$
$N(5; n) = 2 \times N(5; n - 2), \qquad n \geq 3 \tag{5}$
$N(5; 2n + 1) = T(5; 2n + 1) = 0, \qquad n \geq 0 \tag{6}$