Formulas¶
$N(w; h)$ - number of ways to tile $w\times h$ rectangle (including symmetric solutions)
$T(w; h) = \begin{cases} 1, & N(w; h) \geq 1 \\ 0, & \text{else} \end{cases}$ - tileability function, $1$ if tiles rectangle, $0$ otherwise
$A(w; h) = \left(N(w; h)\right)^{\frac{1}{wh}}$ - average number of ways to tile cell in $w\times h$ rectangle (including symmetric solutions)
$G(T; x; y) = \sum_{w=1}^{\infty}\sum _{h=1}^{\infty}T(w; h)x^wy^h$ - bivariate generating function of $T(w; h)$
$G(A; x; y) = \sum_{w=1}^{\infty}\sum _{h=1}^{\infty}A(w; h)x^wy^h$ - bivariate generating function of $A(w; h)$
$N(1; n) = T(1; n) = 0 \tag{1}$
$N(2; n) = T(2; n) = 0 \tag{2}$
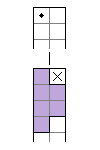
$N(3; n) = T(3; n) = 0 \tag{3}$
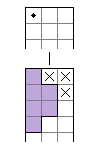
$N(7; n) = T(7; n) = 0 \tag{4}$
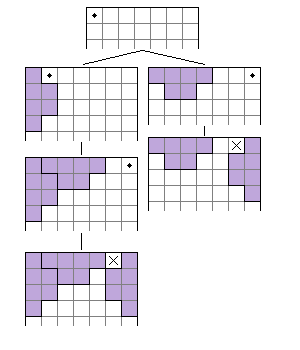
$N(n; m) = T(n; m) = 0, \qquad 6\nmid n,6\nmid m \tag{5}$
Assume D hexomino tiles $n\times m$ rectangles for $6\nmid n,6\nmid m$.
Place numbers in rectangles' cells according to function $F(x,y)\equiv (-1)^{\left\lfloor\frac{y}{3}\right\rfloor+x}+(-1)^{\left\lfloor\frac{x}{3}\right\rfloor+y}+2-2(-1)^{x+y}\pmod{12}$, where $x$ and $y$ are cells' coordinates (zero-based). On the one hand, D hexomino, no matter how placed, covers sum congruent to $0\pmod{12}$. Then sum covered by all hexominoes is also congruent to $0\pmod{12}$. On the other hand, rectangle covers sum congruent to $\sum_{x=0}^{n-1}\sum_{y=0}^{m-1}F(x,y)$, which is not congruent to $0\pmod{12}$ for $6\nmid n,6\nmid m$. Contradiction, as hexomino tiles this rectangle and thus sum covered by all hexominoes should be equal to sum covered by rectangle. Thus only assumption we made is false - D hexomino doesn't tile $n\times m$ rectangles for $6\nmid n,6\nmid m$. Q.E.D.
$N(n; m) = T(n; m) = 0, \qquad 4\nmid n,4\nmid m \tag{6}$
Proved in [1].
Attributions¶
- Michael Reid, Klarner Systems and Tiling Boxes with Polyominoes, Journal of Combinatorial Theory, Series A 111 (2005), no. 1, pp. 89-105. (http://www.cflmath.com/~reid/Research/Ksystem/index.html)